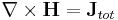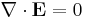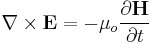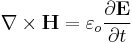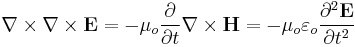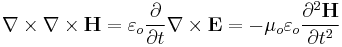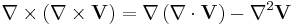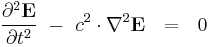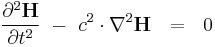A Dynamical Theory of the Electromagnetic Field

A dynamical theory of the electromagnetic field  
Author(s) James Clerk Maxwell
Language English
Subject(s) Classical electromagnetism
Genre(s) Scientific paper
Publisher Philosophical Transactions of the Royal Society
Publication date 1865

"A Dynamical Theory of the Electromagnetic Field" is the third of James Clerk Maxwell's papers regarding electromagnetism, published in 1865.[1] It is the paper in which the original set of four Maxwell's equations first appeared. The concept of displacement current, which he had introduced in his 1861 paper "On Physical Lines of Force", was utilized for the first time, to derive the electromagnetic wave equation.[2]

Contents

Maxwell's original equations

In part III of "A Dynamical Theory of the Electromagnetic Field", which is entitled "General Equations of the Electromagnetic Field", Maxwell formulated twenty equations[1] which were to become known as Maxwell's equations, until this term became applied instead to a set of four vectorized equations selected in 1884 by Oliver Heaviside, which had all appeared in "On physical lines of force".[2]

Heaviside's versions of Maxwell's equations are distinct by virtue of the fact that they are written in modern vector notation. They actually only contain one of the original eight—equation "G" (Gauss's Law). Another of Heaviside's four equations is an amalgamation of Maxwell's law of total currents (equation "A") with Ampère's circuital law (equation "C"). This amalgamation, which Maxwell himself had actually originally made at equation (112) in "On Physical Lines of Force", is the one that modifies Ampère's Circuital Law to include Maxwell's displacement current.[2]

Eighteen of the twenty original Maxwell's equations can be vectorized into 6 equations. Each vectorized equation represents 3 original equations in component form. Including the other two equations, in modern vector notation, they can form a set of eight equations. They are listed below:

(A) The law of total currents
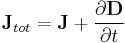
\mathbf{J}_{tot} = \mathbf{J} %2B \frac{\partial\mathbf{D}}{\partial t}
(B) Definition of the magnetic potential
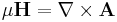
\mu \mathbf{H} = \nabla \times \mathbf{A}
(C) Ampère's circuital law
\nabla \times \mathbf{H} = \mathbf{J}_{tot}
(D) The Lorentz force
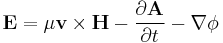
\mathbf{E} = \mu \mathbf{v} \times \mathbf{H} - \frac{\partial\mathbf{A}}{\partial t}-\nabla \phi
This force represents the effect of electric fields created by convection, induction, and by charges.
(E) The electric elasticity equation
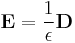
\mathbf{E} = \frac{1}{\epsilon} \mathbf{D}
(F) Ohm's law
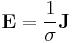
\mathbf{E} = \frac{1}{\sigma} \mathbf{J}
(G) Gauss's law
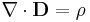
\nabla \cdot \mathbf{D} = \rho
(H) Equation of continuity of charge
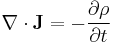
\nabla \cdot \mathbf{J} = -\frac{\partial\rho}{\partial t}
Notation
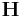\mathbf{H} is the magnetic field, which Maxwell called the "magnetic intensity".
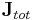\mathbf{J} is the electric current density (with \mathbf{J}_{tot} being the total current including displacement current).
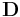\mathbf{D} is the displacement field (called the "electric displacement" by Maxwell).
\rho is the free charge density (called the "quantity of free electricity" by Maxwell).
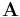\mathbf{A} is the magnetic potential (called the "angular impulse" by Maxwell).
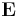\mathbf{E} is the electric field (called the "electromotive force" by Maxwell, not to be confused with the scalar quantity that is now called electromotive force).
\phi is the electric potential (which Maxwell also called "electric potential").
\sigma is the electrical conductivity (Maxwell called the inverse of conductivity the "specific resistance", what is now called the resistivity).

Maxwell did not consider completely general materials; his initial formulation used linear, isotropic, nondispersive permittivity ε and permeability μ, although he also discussed the possibility of anisotropic materials.

It is of particular interest to note that Maxwell includes a 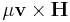\mu \mathbf{v} \times \mathbf{H} term in his expression for the "electromotive force" at equation "D", which corresponds to the magnetic force per unit charge on a moving conductor with velocity 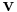\mathbf{v}. This means that equation "D" is effectively the Lorentz force. This equation first appeared at equation (77) in "On Physical Lines of Force" quite some time before Lorentz thought of it.[2] Nowadays, the Lorentz force sits alongside Maxwell's equations as an additional electromagnetic equation that is not included as part of the set.

When Maxwell derives the electromagnetic wave equation in his 1864 paper, he uses equation "D" as opposed to using Faraday's law of electromagnetic induction as in modern textbooks. Maxwell however drops the 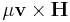\mu \mathbf{v} \times \mathbf{H} term from equation "D" when he is deriving the electromagnetic wave equation, and he considers the situation only from the rest frame.

Maxwell – First to propose that light is an electromagnetic wave

In "A dynamical theory of the electromagnetic field", Maxwell utilized the correction to Ampère's Circuital Law that he had made in part III of "On physical lines of force".[1] In part VI of his 1864 paper "Electromagnetic theory of light", Maxwell combined displacement current with some of the other equations of electromagnetism and obtained a wave equation with a speed equal to the speed of light. He commented,

The agreement of the results seems to show that light and magnetism are affections of the same substance, and that light is an electromagnetic disturbance propagated through the field according to electromagnetic laws.

Maxwell's derivation of the electromagnetic wave equation has been replaced in modern physics by a much less cumbersome method which combines the corrected version of Ampère's Circuital Law with Faraday's law of electromagnetic induction.

To obtain the electromagnetic wave equation in a vacuum using the modern method, we begin with the modern 'Heaviside' form of Maxwell's equations. Using (SI units) in a vacuum, these equations are

\nabla \cdot \mathbf{E} = 0
\nabla \times \mathbf{E} = -\mu_o \frac{\partial \mathbf{H}} {\partial t}
\nabla \cdot \mathbf{H} = 0
\nabla \times \mathbf{H} =\varepsilon_o \frac{ \partial \mathbf{E}} {\partial t}

If we take the curl of the curl equations we obtain

\nabla \times \nabla \times \mathbf{E} = -\mu_o \frac{\partial } {\partial t} \nabla \times \mathbf{H} = -\mu_o \varepsilon_o \frac{\partial^2 \mathbf{E} } {\partial t^2}
\nabla \times \nabla \times \mathbf{H} = \varepsilon_o \frac{\partial } {\partial t} \nabla \times \mathbf{E} = -\mu_o \varepsilon_o \frac{\partial^2 \mathbf{H} } {\partial t^2}

If we note the vector identity

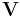\nabla \times \left( \nabla \times \mathbf{V} \right) = \nabla \left( \nabla \cdot \mathbf{V} \right) - \nabla^2 \mathbf{V}

where \mathbf{V} is any vector function of space, we recover the wave equations

{\partial^2 \mathbf{E} \over \partial t^2} \ - \ c^2 \cdot \nabla^2 \mathbf{E} \ \ = \ \ 0
{\partial^2 \mathbf{H} \over \partial t^2} \ - \ c^2 \cdot \nabla^2 \mathbf{H} \ \ = \ \ 0

where

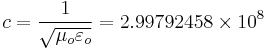c = { 1 \over \sqrt{ \mu_o \varepsilon_o } } = 2.99792458 \times 10^8 meters per second

is the speed of light in free space.

See also

Book: Maxwell's equations
Wikipedia books are collections of articles that can be downloaded or ordered in print.

References

  1. ^ a b c Maxwell, James Clerk (1865). "A dynamical theory of the electromagnetic field" (PDF). Philosophical Transactions of the Royal Society of London 155: 459–512. doi:10.1098/rstl.1865.0008. http://upload.wikimedia.org/wikipedia/commons/1/19/A_Dynamical_Theory_of_the_Electromagnetic_Field.pdf.  (This article accompanied a December 8, 1864 presentation by Maxwell to the Royal Society.)
  2. ^ a b c d Maxwell, James Clerk (1861). "On physical lines of force" (PDF). Philosophical Magazine. http://upload.wikimedia.org/wikipedia/commons/b/b8/On_Physical_Lines_of_Force.pdf. 

Further reading